Session 20 code

Author

Carolyn Koehn

Load libraries:

Code

library(sf)
library(spdep)
library(tidyverse)
library(tmap)

Load data:

Code

cdc <- read_sf("/opt/data/data/vectorexample/cdc_nw.shp") %>% 
  select(stateabbr, countyname, countyfips, casthma_cr)

plot(cdc["casthma_cr"])

Find neighbors based on contiguity

Code

nb.qn <- poly2nb(cdc, queen = TRUE)
nb.rk <- poly2nb(cdc, queen = FALSE)

visualize

Code

par(mfrow=c(1,2))
plot(st_geometry(cdc), border = 'lightgrey')
plot(nb.qn, st_coordinates(st_centroid(cdc)), add=TRUE, col='red', main="Queen's case")
plot(st_geometry(cdc), border = 'lightgrey')
plot(nb.rk, st_coordinates(st_centroid(cdc)), add=TRUE, col='blue', main="Rook's case")

Code

par(mfrow=c(1,1))

Get weights

Code

lw.qn <- nb2listw(nb.qn, style="W", zero.policy = TRUE)

lw.qn$weights[1:5]

[[1]]
[1] 0.5 0.5

[[2]]
[1] 0.25 0.25 0.25 0.25

[[3]]
[1] 0.2 0.2 0.2 0.2 0.2

[[4]]
[1] 0.3333333 0.3333333 0.3333333

[[5]]
[1] 1

Get distance

Code

asthma.lag <- lag.listw(lw.qn, cdc$casthma_cr)

head(asthma.lag)

[1] 10.30000  9.57500  9.88000 10.26667  9.50000  9.90000

Get Moran’s I

Code

M <- lm(asthma.lag ~ cdc$casthma_cr)

M


Call:
lm(formula = asthma.lag ~ cdc$casthma_cr)

Coefficients:
   (Intercept)  cdc$casthma_cr  
        3.7209          0.6357

Code

plot(x = cdc$casthma_cr, y = asthma.lag)
abline(M$coefficients[1], M$coefficients[2], col="red")

Compare to null hypothesis

Code

n <- 400L   # Define the number of simulations
I.r <- vector(length=n)  # Create an empty vector

for (i in 1:n){
  # Randomly shuffle asthma values
  x <- sample(cdc$casthma_cr, replace=FALSE)
  # Compute new set of lagged values
  x.lag <- lag.listw(lw.qn, x)
  # Compute the regression slope and store its value
  M.r    <- lm(x.lag ~ x)
  I.r[i] <- coef(M.r)[2]
}

Moran test code

moran.test uses a few key assumptions, including that the data is normally distributed

Code

moran.test(cdc$casthma_cr, lw.qn)


    Moran I test under randomisation

data:  cdc$casthma_cr  
weights: lw.qn  
n reduced by no-neighbour observations  

Moran I statistic standard deviate = 40.826, p-value < 2.2e-16
alternative hypothesis: greater
sample estimates:
Moran I statistic       Expectation          Variance 
     0.6381428057     -0.0005037783      0.0002447034

Find neighbors based on distance

Code

cdc.pt <- st_point_on_surface(cdc)

Warning: st_point_on_surface assumes attributes are constant over geometries

Warning in st_point_on_surface.sfc(st_geometry(x)): st_point_on_surface may not
give correct results for longitude/latitude data

Code

# another option is st_centroid

# get nearest neighbor for each point
geog.nearnb <- knn2nb(knearneigh(cdc.pt, k=1))

# get list of nearest neighbors so that every tract has at least one neighbor
nb.nearest <- dnearneigh(cdc.pt,
                         d1 = 0,
                         d2 = max(unlist(nbdists(geog.nearnb, cdc.pt))))

Get weights and distance

Code

lw.nearest <- nb2listw(nb.nearest, style="W")
asthma.lag <- lag.listw(lw.nearest, cdc$casthma_cr)

Calculate Moran’s I

Code

M2 <- lm(asthma.lag ~ cdc$casthma_cr)

M2


Call:
lm(formula = asthma.lag ~ cdc$casthma_cr)

Coefficients:
   (Intercept)  cdc$casthma_cr  
        8.8547          0.1578

visualize:

Code

plot(x = cdc$casthma_cr, y = asthma.lag)
abline(M2$coefficients[1], M2$coefficients[2], col="red")

Simulate data under null hypothesis

Code

n <- 400L   # Define the number of simulations
I.r <- vector(length=n)  # Create an empty vector

for (i in 1:n){
  # Randomly shuffle asthma values
  x <- sample(cdc$casthma_cr, replace=FALSE)
  # Compute new set of lagged values - use new neighbors!
  x.lag <- lag.listw(lw.nearest, x)
  # Compute the regression slope and store its value
  M.r    <- lm(x.lag ~ x)
  I.r[i] <- coef(M.r)[2]
}

Closer look at simulation

Code

i <- 1
I.r <- vector(length=n)  # Create an empty vector

# Randomly shuffle asthma values
x <- sample(cdc$casthma_cr, replace=FALSE)

random_data <- cbind(cdc, x)

plot(random_data["x"])

Code

# Compute new set of lagged values
x.lag <- lag.listw(lw.nearest, x)

head(x.lag)

[1] 10.61818 10.50821 10.51805 10.48258 10.45769 10.51111

Code

# Compute the regression slope and store its value
M.r    <- lm(x.lag ~ x)
I.r[i] <- coef(M.r)[2]
  
head(I.r)

[1] -0.002479055  0.000000000  0.000000000  0.000000000  0.000000000
[6]  0.000000000

Do it with new data

Code

cejst <- st_read("/opt/data/data/assignment01/cejst_nw.shp")

cejst.id <- cejst %>%
  filter(SF == "Idaho") %>%
  select(CF, SF, EPLR_PFS)

After this, we tried our hand at tackling the homework questions with the cejst data individually.

Use the nearest-neighbor approach that we used in class to estimate the lagged values for the cejst dataset and estimate the slope of the line describing Moran’s I statistic.

Now use the permutation approach to compare your measured value to one generated from multiple simulations. Generate the plot of the data. Do you see more evidence of spatial autocorrelation?

--- title: "Session 20 code" author: "Carolyn Koehn" format: html --- Load libraries: ```{r} #| message: false #| warning: false library(sf) library(spdep) library(tidyverse) library(tmap) ``` Load data: ```{r} #| eval: false cdc <- read_sf("/opt/data/data/vectorexample/cdc_nw.shp") %>% select(stateabbr, countyname, countyfips, casthma_cr) plot(cdc["casthma_cr"]) ``` ```{r} #| include: false cdc <- read_sf("C:/Users/carolynkoehn/Documents/HES505_Fall_2024/data/2023/vectorexample/cdc_nw.shp") %>% select(stateabbr, countyname, countyfips, casthma_cr) plot(cdc["casthma_cr"]) ``` ## Find neighbors based on contiguity ```{r} nb.qn <- poly2nb(cdc, queen = TRUE) nb.rk <- poly2nb(cdc, queen = FALSE) ``` 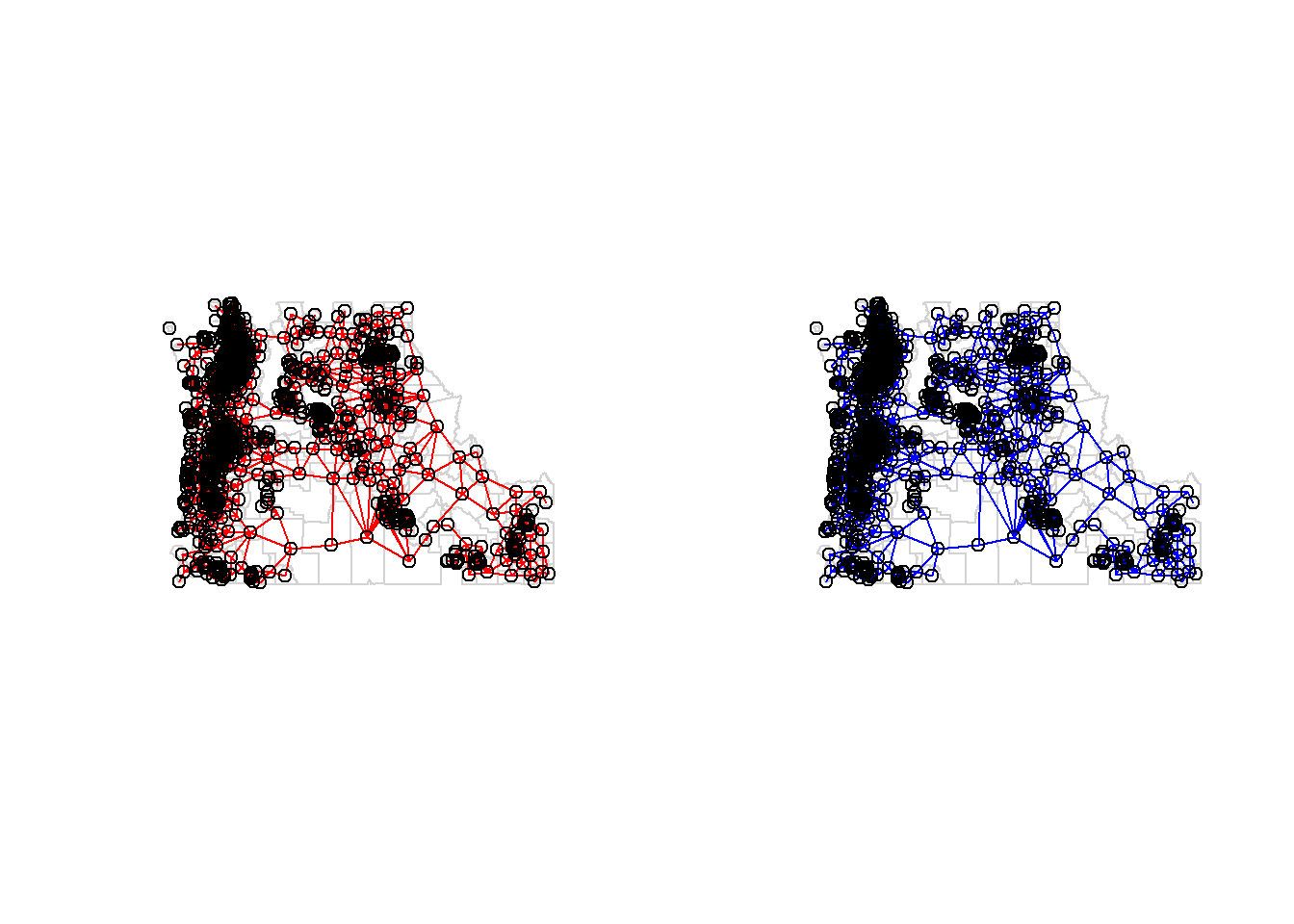visualize ```{r} #| warning: false par(mfrow=c(1,2)) plot(st_geometry(cdc), border = 'lightgrey') plot(nb.qn, st_coordinates(st_centroid(cdc)), add=TRUE, col='red', main="Queen's case") plot(st_geometry(cdc), border = 'lightgrey') plot(nb.rk, st_coordinates(st_centroid(cdc)), add=TRUE, col='blue', main="Rook's case") par(mfrow=c(1,1)) ``` ### Get weights ```{r} lw.qn <- nb2listw(nb.qn, style="W", zero.policy = TRUE) lw.qn$weights[1:5] ``` ### Get distance ```{r} asthma.lag <- lag.listw(lw.qn, cdc$casthma_cr) head(asthma.lag) ``` ### Get Moran's I ```{r} M <- lm(asthma.lag ~ cdc$casthma_cr) M ``` ```{r} plot(x = cdc$casthma_cr, y = asthma.lag) abline(M$coefficients[1], M$coefficients[2], col="red") ``` ### Compare to null hypothesis ```{r} n <- 400L # Define the number of simulations I.r <- vector(length=n) # Create an empty vector for (i in 1:n){ # Randomly shuffle asthma values x <- sample(cdc$casthma_cr, replace=FALSE) # Compute new set of lagged values x.lag <- lag.listw(lw.qn, x) # Compute the regression slope and store its value M.r <- lm(x.lag ~ x) I.r[i] <- coef(M.r)[2] } ``` ### Moran test code `moran.test` uses a few key assumptions, including that the data is normally distributed ```{r} moran.test(cdc$casthma_cr, lw.qn) ``` ## Find neighbors based on distance ```{r} cdc.pt <- st_point_on_surface(cdc) # another option is st_centroid # get nearest neighbor for each point geog.nearnb <- knn2nb(knearneigh(cdc.pt, k=1)) # get list of nearest neighbors so that every tract has at least one neighbor nb.nearest <- dnearneigh(cdc.pt, d1 = 0, d2 = max(unlist(nbdists(geog.nearnb, cdc.pt)))) ``` ### Get weights and distance ```{r} lw.nearest <- nb2listw(nb.nearest, style="W") asthma.lag <- lag.listw(lw.nearest, cdc$casthma_cr) ``` ### Calculate Moran's I ```{r} M2 <- lm(asthma.lag ~ cdc$casthma_cr) M2 ``` visualize: ```{r} plot(x = cdc$casthma_cr, y = asthma.lag) abline(M2$coefficients[1], M2$coefficients[2], col="red") ``` ### Simulate data under null hypothesis ```{r} n <- 400L # Define the number of simulations I.r <- vector(length=n) # Create an empty vector for (i in 1:n){ # Randomly shuffle asthma values x <- sample(cdc$casthma_cr, replace=FALSE) # Compute new set of lagged values - use new neighbors! x.lag <- lag.listw(lw.nearest, x) # Compute the regression slope and store its value M.r <- lm(x.lag ~ x) I.r[i] <- coef(M.r)[2] } ``` #### Closer look at simulation ```{r} i <- 1 I.r <- vector(length=n) # Create an empty vector # Randomly shuffle asthma values x <- sample(cdc$casthma_cr, replace=FALSE) random_data <- cbind(cdc, x) plot(random_data["x"]) # Compute new set of lagged values x.lag <- lag.listw(lw.nearest, x) head(x.lag) # Compute the regression slope and store its value M.r <- lm(x.lag ~ x) I.r[i] <- coef(M.r)[2] head(I.r) ``` ## Do it with new data ```{r} #| eval: false cejst <- st_read("/opt/data/data/assignment01/cejst_nw.shp") cejst.id <- cejst %>% filter(SF == "Idaho") %>% select(CF, SF, EPLR_PFS) ``` ```{r} #| include: false cejst <- st_read("C:/Users/carolynkoehn/Documents/HES505_Fall_2024/data/2023/assignment01/cejst_nw.shp") cejst.id <- cejst %>% filter(SF == "Idaho") %>% select(CF, SF, EPLR_PFS) ``` After this, we tried our hand at tackling the homework questions with the `cejst` data individually. Use the nearest-neighbor approach that we used in class to estimate the lagged values for the cejst dataset and estimate the slope of the line describing Moran's I statistic. Now use the permutation approach to compare your measured value to one generated from multiple simulations. Generate the plot of the data. Do you see more evidence of spatial autocorrelation?